动态规划五步
| 问题 |
解决 |
| 下标/数组的含义 |
一般是容量 |
| 递推公式 |
找规律 |
| 初始化 |
看条件 |
| 遍历数组 |
2层for循环要注意谁在外 |
| 打印数组 |
查错 |
当时做的时候,有点问题
整数拆分
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
示例 1:
输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
解
一个整数怎么拆才能乘积最大 比如 3 -> 2|1 21=2 4-> 2|2 22=4
遍历一个一个的拆 将一个数先拆成 1 和 n-1 再试试 2 和 n-2
dp[i]=Math.max(Math.max(j*(i-j),j*dp[i-j]),dp[i])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution {
public int integerBreak(int n) {
int[] dp=new int[n+1];
dp[2]=1;
for(int i=3;i<=n;i++){
for(int j=1;j<i;j++){
dp[i]=Math.max(Math.max(j*(i-j),j*dp[i-j]),dp[i]);
}
}
return dp[n];
}
}
|
不同的二叉搜索树
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。

三个节点的 累加 左面节点数从0涨到3-1个累加 如果左边节点数是2个的话 则有dp[2]个 同理右边也是 左右两边相乘
dp[i]+=dp[j]*dp[i-j-1];
1
2
3
4
5
6
7
8
9
10
11
12
13
| class Solution {
public int numTrees(int n) {
int[] dp=new int[n+1];
dp[0]=1;dp[1]=1;
for(int i=2;i<=n;i++){
for(int j=0;j<i;j++){
dp[i]+=dp[j]*dp[i-j-1];
}
}
return dp[n];
}
}
|
分割等和子集
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
示例 1:
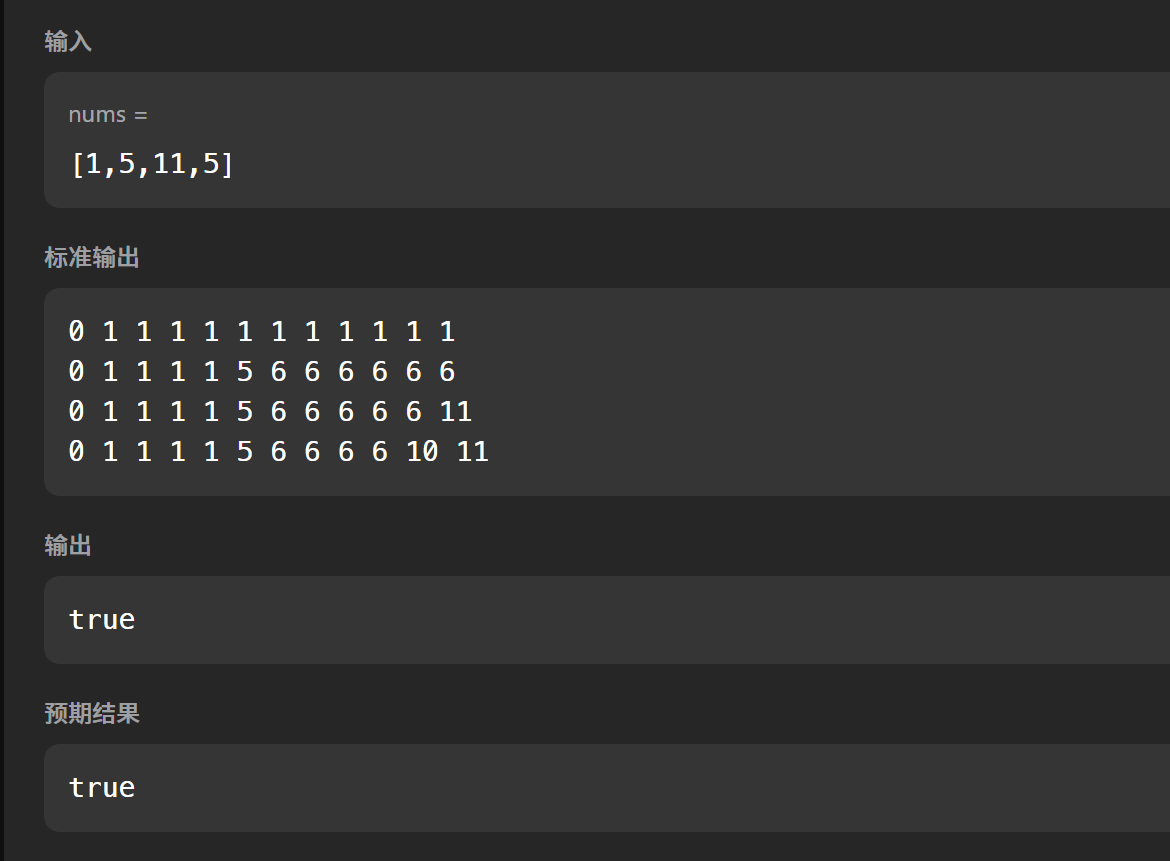
输入:nums = [1,5,11,5]
输出:true
解释:数组可以分割成 [1, 5, 5] 和 [11] 。
示例 2:
输入:nums = [1,2,3,5]
输出:false
解释:数组不能分割成两个元素和相等的子集。
二维dp数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public boolean canPartition(int[] nums) {
int sum=0;
for(int i=0;i<nums.length;i++)sum+=nums[i];
if(sum%2!=0)return false;
int[][] dp=new int[nums.length+1][sum/2+1];
for(int i=0;i<nums.length+1;i++)dp[i][0]=0;
for(int i=0;i<sum/2+1;i++)dp[0][i]=0;
for(int i=1;i<nums.length+1;i++){
for(int j=1;j<sum/2+1;j++){
if(nums[i-1]>j){
dp[i][j]=dp[i-1][j];
}else{
dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-nums[i-1]]+nums[i-1]);
if(dp[i][j]==sum/2)return true;
}
}
}
return dp[nums.length][sum/2]==sum/2;
}
}
|
一维dp数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution {
public boolean canPartition(int[] nums) {
int sum=0;
for(int i=0;i<nums.length;i++)sum+=nums[i];
if(sum%2==1)return false;
int[] dp=new int[sum/2+1];
for(int i=0;i<nums.length;i++)
for(int j=dp.length-1;j>=nums[i];j--){
dp[j]=Math.max(dp[j],dp[j-nums[i]]+nums[i]);
if(dp[j]==sum/2)return true;
}
return false;
}
}
|
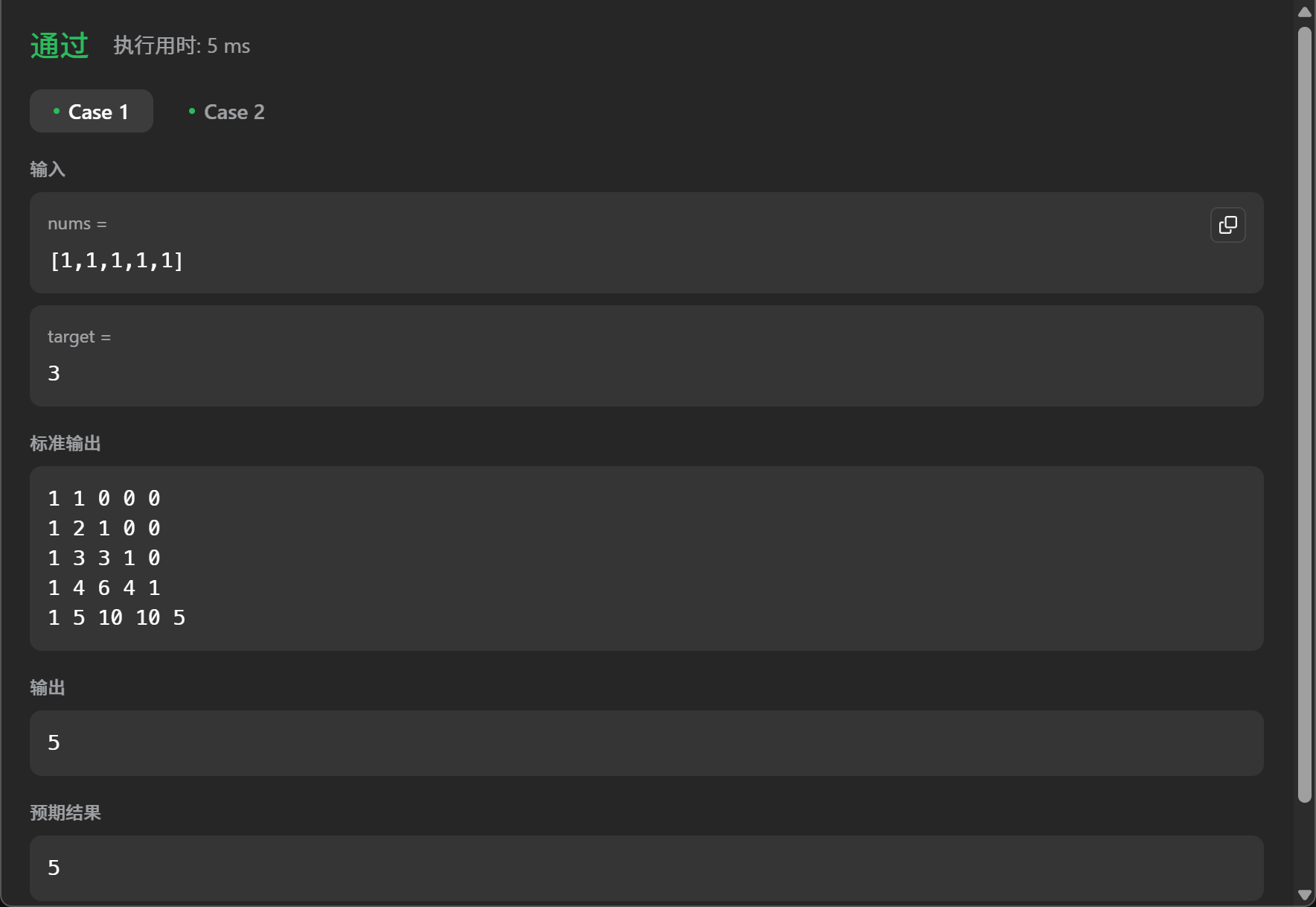
目标和
给你一个非负整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 ‘+’ 或 ‘-‘ ,然后串联起所有整数,可以构造一个 表达式 :
例如,nums = [2, 1] ,可以在 2 之前添加 ‘+’ ,在 1 之前添加 ‘-‘ ,然后串联起来得到表达式 “+2-1” 。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| class Solution {
public int findTargetSumWays(int[] nums, int target) {
int sum=0;
for(int i=0;i<nums.length;i++)sum+=nums[i];
if(sum<Math.abs(target))return 0;
if((sum+target)%2==1)return 0;
int n=(sum+target)/2;
int[] dp=new int[n+1];
dp[0]=1;
for(int i=0;i<nums.length;i++)
for(int j=n;j>=nums[i];j--)
dp[j]+=dp[j-nums[i]];
return dp[n];
}
}
|
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
示例 1:
输入:strs = [“10”, “0001”, “111001”, “1”, “0”], m = 5, n = 3
输出:4
解释:最多有 5 个 0 和 3 个 1 的最大子集是 {“10”,”0001”,”1”,”0”} ,因此答案是 4 。
其他满足题意但较小的子集包括 {“0001”,”1”} 和 {“10”,”1”,”0”} 。{“111001”} 不满足题意,因为它含 4 个 1 ,大于 n 的值 3 。
示例 2:
输入:strs = [“10”, “0”, “1”], m = 1, n = 1
输出:2
解释:最大的子集是 {“0”, “1”} ,所以答案是 2 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| class Solution {
public int findMaxForm(String[] strs, int m, int n) {
int[][] dp=new int[m+1][n+1];
for(String s:strs){
int x=0,y=0;
for(int i=0;i<s.length();i++)
if(s.charAt(i)=='0')
x++;
else y++;
for(int i=m;i>=x;i--){
for(int j=n;j>=y;j--){
dp[i][j]=Math.max(dp[i][j],dp[i-x][j-y]+1);
}
}
}
return dp[m][n];
}
}
|
单词拆分
给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单词拼接出 s 则返回 true。
注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
示例 1:
输入: s = “leetcode”, wordDict = [“leet”, “code”]
输出: true
解释: 返回 true 因为 “leetcode” 可以由 “leet” 和 “code” 拼接成。
示例 2:
输入: s = “applepenapple”, wordDict = [“apple”, “pen”]
输出: true
解释: 返回 true 因为 “applepenapple” 可以由 “apple” “pen” “apple” 拼接成。
注意,你可以重复使用字典中的单词。
示例 3:
输入: s = “catsandog”, wordDict = [“cats”, “dog”, “sand”, “and”, “cat”]
输出: false
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| class Solution {
public boolean wordBreak(String s, List<String> wordDict) {
boolean[] dp=new boolean[s.length()+1];
dp[0]=true;
for(int i=1;i<s.length()+1;i++)
for(int j=0;j<i;j++)
if(wordDict.indexOf(s.substring(j,i))!=-1&&dp[j])
dp[i]=true;
return dp[s.length()];
}
}
|
打家劫舍Ⅲ
小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为 root 。
除了 root 之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ,房屋将自动报警。
给定二叉树的 root 。返回 在不触动警报的情况下 ,小偷能够盗取的最高金额 。
示例 1:

输入: root = [3,2,3,null,3,null,1]
输出: 7
解释: 小偷一晚能够盗取的最高金额 3 + 3 + 1 = 7
示例 2:

输入: root = [3,4,5,1,3,null,1]
输出: 9
解释: 小偷一晚能够盗取的最高金额 4 + 5 = 9
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
class Solution {
public int rob(TreeNode root) {
int[] dp=a(root);
return Math.max(dp[0],dp[1]);
}
private int[] a(TreeNode root){
int[] dp=new int[2];
if(root==null)return dp;
int[] left=a(root.left);
int[] right=a(root.right);
dp[1]=root.val+left[0]+right[0];
dp[0]=Math.max(left[0],left[1])+Math.max(right[0],right[1]);
return dp;
}
}
|
买卖股票的最佳时机Ⅲ
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:prices = [3,3,5,0,0,3,1,4]
输出:6
解释:在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。
随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3 。
示例 2:
输入:prices = [1,2,3,4,5]
输出:4
解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。
因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这个情况下, 没有交易完成, 所以最大利润为 0。
示例 4:
输入:prices = [1]
输出:0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution {
public int maxProfit(int[] prices) {
int n=prices.length;
int[][] dp=new int[n][5];
dp[0][0]=0;
dp[0][1]=-prices[0];
dp[0][2]=0;
dp[0][3]=-prices[0];
dp[0][4]=0;
for(int i=1;i<n;i++){
dp[i][1]=Math.max(dp[i-1][0]-prices[i],dp[i-1][1]);
dp[i][2]=Math.max(dp[i-1][2],dp[i-1][1]+prices[i]);
dp[i][3]=Math.max(dp[i-1][3],dp[i-1][2]-prices[i]);
dp[i][4]=Math.max(dp[i-1][4],dp[i-1][3]+prices[i]);
}
return dp[n-1][4];
}
}
|
买卖股票得最佳时机Ⅳ
给你一个整数数组 prices 和一个整数 k ,其中 prices[i] 是某支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说,你最多可以买 k 次,卖 k 次。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:k = 2, prices = [2,4,1]
输出:2
解释:在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2 。
示例 2:
输入:k = 2, prices = [3,2,6,5,0,3]
输出:7
解释:在第 2 天 (股票价格 = 2) 的时候买入,在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。
随后,在第 5 天 (股票价格 = 0) 的时候买入,在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution {
public int maxProfit(int k, int[] prices) {
int n=prices.length;
int[][] dp=new int[n][k*2+1];
for(int i=1;i<k*2+1;i+=2)dp[0][i]=-prices[0];
for(int i=1;i<n;i++){
for(int j=1;j<k*2+1;j+=2){
dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-1]-prices[i]);
dp[i][j+1]=Math.max(dp[i-1][j+1],dp[i-1][j]+prices[i]);
}
}
return dp[n-1][k*2];
}
}
|
买卖股票的最佳时机含冷冻期
给定一个整数数组prices,其中第 prices[i] 表示第 i 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: prices = [1,2,3,0,2]
输出: 3
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]
示例 2:
输入: prices = [1]
输出: 0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| class Solution {
public int maxProfit(int[] prices) {
int n=prices.length;
int[][] dp=new int[n][4];
dp[0][0]=-prices[0];
dp[0][1]=0;
dp[0][2]=0;
dp[0][3]=0;
for(int i=1;i<n;i++){
dp[i][0]=Math.max(dp[i-1][0],Math.max(dp[i-1][3]-prices[i],dp[i-1][1]-prices[i]));
dp[i][1]=Math.max(dp[i-1][1],dp[i-1][3]);
dp[i][2]=dp[i-1][0]+prices[i];
dp[i][3]=dp[i-1][2];
}
return Math.max(dp[n-1][1],Math.max(dp[n-1][2],dp[n-1][3]));
}
}
|





